IFC - Industry Foundation Classes/IFC alignment
In road and railway design, the alignment model provides a geometric description of a long linear infrastructure work, e.g a road or railway. In IFC4X1 IfcAlignment was first introduced, but significantly reworked in the context of the IFC4.3 IfcRail project.
In IfcOpenShell support for alignment geometry is still in progress and scheduled for v0.8
- https://github.com/IfcOpenShell/IfcOpenShell/issues/842
- https://github.com/IfcOpenShell/IfcOpenShell/pull/1470
- https://github.com/IfcOpenShell/IfcOpenShell/pull/3148
IFC distinguishes the semantic (or business logic) of the alignment and the geometric representation, overlapping significantly in content. Relevant concepts from the specification:
- https://ifc43-docs.standards.buildingsmart.org/IFC/RELEASE/IFC4x3/HTML/concepts/Object_Composition/Nesting/Alignment_Layout/content.html
- https://ifc43-docs.standards.buildingsmart.org/IFC/RELEASE/IFC4x3/HTML/concepts/Product_Shape/Product_Geometric_Representation/Alignment_Geometry/Alignment_Geometry_Cant/content.html
Introduction to Highway Alignment Modeling with IfcOpenShell[edit]
This post introduces the basic concepts of horizontal and vertical alignments for highway applications, highlights how alignments are realized using buildingSMART International’s IFC 4.3.2 Schema, and provides example programs based on the IfcOpenShell library.
The primary objectives are to demystify the IFC 4.3.2 alignment model and to illustrate techniques to create alignment models with the IfcOpenShell toolkit using C++ and Python.
Alignment Geometry[edit]
An assumption is made that the reader is familiar with the civil engineering concepts of horizontal and vertical alignments. There are many excellent textbooks that cover the concepts in detail. A freely available text is Bridge Geometry Manual, published by the US Department of Transportation, Federal Highway Administration (FHWA, 2022).
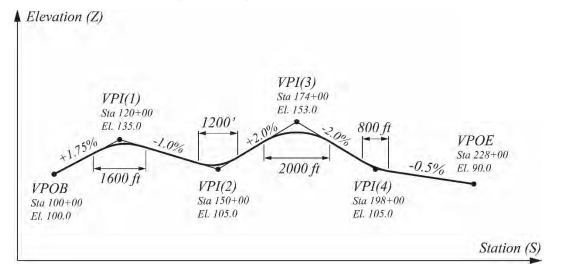
The concepts this post focuses on are horizontal alignment and vertical alignment (sometimes referred to as vertical profile). Railway cant and roadway superelevation are not discussed. The alignment provided in the FHWA Bridge Geometry Manual will serve as an example. The horizontal and vertical alignments are shown in Figure 1 and Figure 2, respectively.
Horizontal Alignment[edit]
A horizontal alignment typically consists of straight lines called tangents that are connect by curves. The curves are usually circular arcs. Easement or transition curves in the form of spirals can be used to provide gradual transitions between tangents and circular curves. There are many types of transition curves utilized in practice, with the most common being the clothoid or Euler spiral.
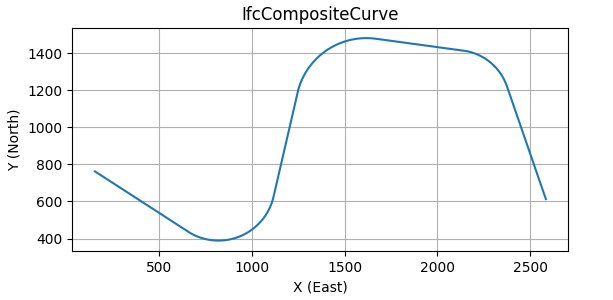
The horizontal alignment is a plan view curvilinear path in a Cartesian coordinate system aligned with East and North. Positions along an alignment, measured along the plan view projection of the 3D curve alignment curve, are denoted with stations or chainage. The example alignment has four tangent runs connected by three horizontal curves. The alignment begins at Station 100+00 and each station is equal to 100 feet in distance along the alignment. The first curve begins at Station 119+56.79 which is 1,956.79 feet, or 19.5679 stations, from the alignment's point of beginning.
Vertical Alignment[edit]
A vertical alignment consists of straight sections of grade lines connected by vertical curves. The vertical curves are typically parabolas or circular arcs, though clothoids or other transition curves are occasionally used. A vertical alignment is defined along the curvilinear path of a horizontal alignment in a Distance Along, Elevation coordinate system. Combined, the horizontal and vertical alignments define a 3D curve. This combination of two 2D curves is sometimes referred to as a 2.5D geometry because the vertical alignment must be projected onto the corresponding distance along the horizontal alignment in order to determine the Z coordinate at any given point of interest.
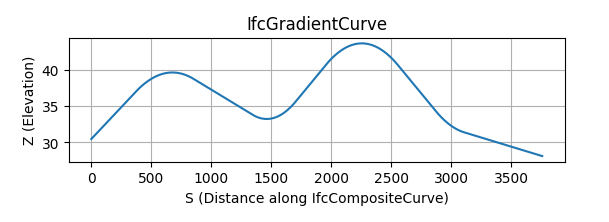
The example vertical alignment consists of five gradients connected by four parabolic vertical curves.
IFC Schema[edit]
It is assumed that the reader is generally familiar with the buildingSMART International Industry Foundation Class (IFC) specification. The IFC specification is a data schema for representing processes and data for the built asset industry. Version 4.3.2.0 of the IFC specification became an ISO standard in 2024. The IFC specification is available on the buildingSMART (buildingSMART International, 2024) web site at https://technical.buildingsmart.org/standards/ifc/ifc-schema-specifications/.
The IFC 4.3.2 schema provides entities for defining horizontal and vertical alignments. An alignment can have a semantic definition (business logic) and a geometric definition.
Semantic Definition[edit]
The semantic definition of alignment allows for the alignment to be described as close as possible to the terminology and concepts used in a business context. Examples include horizontal, vertical and cant layouts, stationing, and anchor points for domain specific properties such as design speed, cant deficiency, superelevation transitions, and widenings.
Specialized applications can analyze alignments using the semantic information. Alignments can be evaluated against design criteria such as speed requirements, sight distances, and maximum gradient, to name a few.
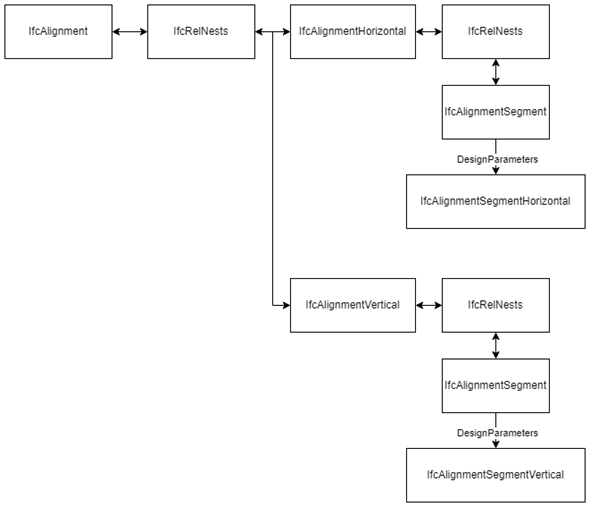
The IfcAlignment semantic definition is composed of an instance of IfcAlignmentHorizontal and IfcAlignmentVertical through an IfcRelNests relationship. The IfcAlignmentHorizontal and IfcAlignmentVertical are in turn composed of one or more IfcAlignmentSegment entities through IfcRelNests relationships. The IfcAlignmentSegment models the segment design parameters in a subtype of IfcAlignmentParameterSegment; IfcAlignmentHorizontalSegment and IfcAlignmentVerticalSegment in this case. The semantic definition model is shown in Figure 3.
An interesting caveat of IfcAlignmentHorizontal and IfcAlignmentVertical (and IfcAlignmentCant) is that the last IfcAlignmentSegment.DesignParameters must be zero length. If a geometric representation is provided, then its corresponding last segment must also be zero length. For a continuous composition of segments, the end of one segment is at the same location as the start of the next segment. The zero-length segment is intended to provide the end point of the last segment.
Geometric Definition[edit]
The semantic definition of an alignment contains a lot of geometric information, such as segment type (line, curve, spiral) and parameters such as length, radius, and gradient. The geometric definition seems somewhat redundant. While related, the semantic definition and geometric definition are independent and serve different purposes.
Since the semantic and geometric definitions of an alignment are so similar, it’s easier to understand the difference by examining a different type of entity. Consider a highway sign. The semantic definition describes an object as a sign that says "Exit 101" with an arrow pointing upwards to the right and it is positioned at a specific location (station and offset) relative to an alignment. The geometric definition describes the sign as a rectangle of certain dimension and thickness and is located precisely at a point X, Y, Z and the face of the sign oriented in a certain plane. The distinction between the business and geometric information is clearer in this example, the same concept of separate business logic and geometric definition are applicable to alignments.
The semantic definition of an alignment describes its business attributes (e.g. design speed) while the geometric definition describes the precise geometry (e.g. line from point A to point B followed by an arc of radius R starting at point B and ending at point C).
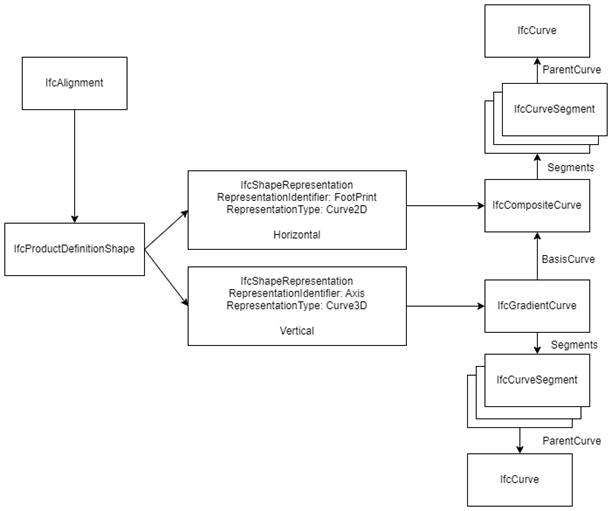
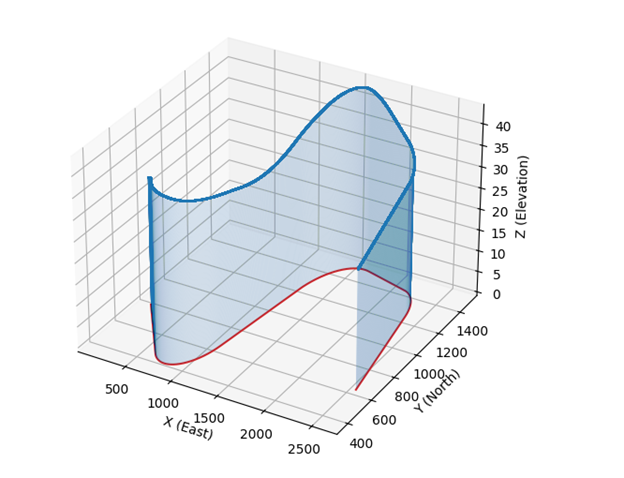
The geometric representation of the IfcAlignment consists of an IfcShapeRepresentation for the plan view horizontal alignment as well as a 3D curve for the combined horizontal and vertical alignment. This is illustrated in Figure 4.
Geometrically, the horizontal alignment is defined by an IfcCompositeCurve and the vertical alignment is defined by an IfcGradientCurve. The horizontal alignment is the basis curve for the vertical alignment.
The horizontal alignment is defined by a sequence of straight tangent runs and circular horizontal curves. Sometimes transition spirals are used as well. For simplicity, transition spirals are not discussed, however the geometric modeling of transition spirals uses the same concepts and mechanisms as the tangents and circular curves illustrated. Once you’ve mastered the basics, adding transition spirals is straightforward.
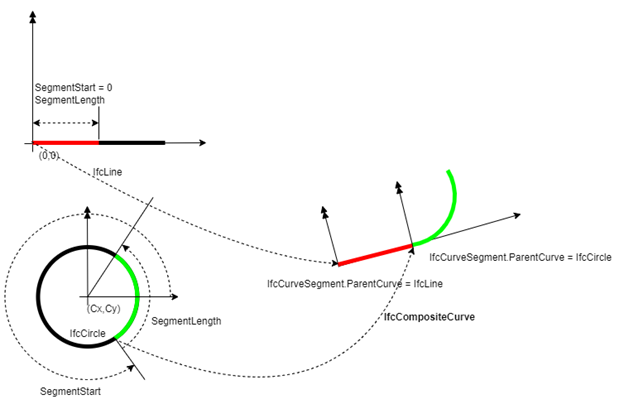
The geometric elements are modeled with IfcCurveSegment. IfcCurveSegment cuts a segment from a parent curve and places it in the alignment coordinate system. A horizontal circular arc is modeled with an IfcCurveSegment that cuts an arc from an IfcCircle. Figure 5 shows an alignment consisting of a tangent run (red) and a horizontal curve (green). The line and curve segments are cut from their IfcLine and IfcCircle parent curves, respectively. The process of defining a parent curve, cutting a segment from that curve, and placing the cut segment into the alignment is repeated to define the entire horizontal and vertical alignments.
All the horizontal alignment IfcCurveSegment objects are then combined to create an IfcCompositeCurve to complete the plan view geometric representation of the horizontal alignment.
A similar process is used to create the vertical alignment. Parent curves are defined and IfcCurveSegment segments are defined that cut a portion of the parent curve and position it in the XY plane where X is distance along the horizontal alignment and Y is elevation. The vertical alignment IfcCurveSegment objects are then used to create an IfcGradientCurve. The IfcGradientCurve uses the horizontal alignment IfcCompositeCurve as its basis curve, which means the horizontal coordinates of the vertical alignment are taken from the horizontal alignment curve as illustrated in Figures 1 and 2.
When defining an IfcCurveSegment, the location and orientation of the parent curve are not particularly important. The Placement attribute of IfcCurveSegment defines the location of the start point of the trimmed curve as well as the orientation of the tangent at the start of the trimmed curve.
IfcOpenShell IFC Toolkit[edit]
IfcOpenShell is an open source (LGPL) software library for working with Industry Foundation Classes (IFC) models. It consists of (a) a core, written in C++, that contains parsing routines and schema information, (b) geometry interpretation functions to translate the bespoke IFC geometry definitions to a universal Open Cascade boundary representation format or CGAL polyhedra (c) python bindings (d) various tools and utilities including BlenderBIM for graphical authoring of models.
The IfcOpenShell IFC toolkit was recently updated to support geometric representations for infrastructure domain entities including IfcAlignment, IfcCompositeCurve and its subtypes, IfcLinearPlacement, and IfcSectionedSolidHorizontal.
Example Alignment Modeling Programs[edit]
Example programs have been developed that construct the alignment model from the FHWA Bridge Geometry Manual document. The programs are implemented in C++ and Python. The source code comments provide a detailed breakdown of the programs.
IfcAlignment.cpp demonstrates the details using IFC to build a basic highway alignment model.
IfcSimplifiedAlignment.cpp constructs the same alignment using the IfcOpenShell alignment utility functions, which greatly reduces the programming effort for typical highway alignments.
Alignment.py replicates the IfcAlignment.cpp C++ program using Python.
The output of the example programs is a file called FHWA_Bridge_Geometry_Alignment_Example.ifc. The geometry created by IfcOpenShell is shown in the following figures: Figure 6 is the alignment plan view, Figure 7 is the vertical profile view, and Figure 8 is a 3D representation of the alignment.
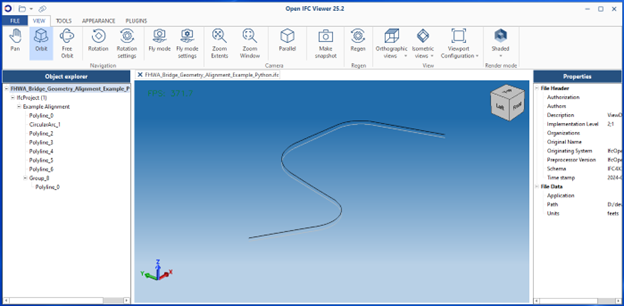
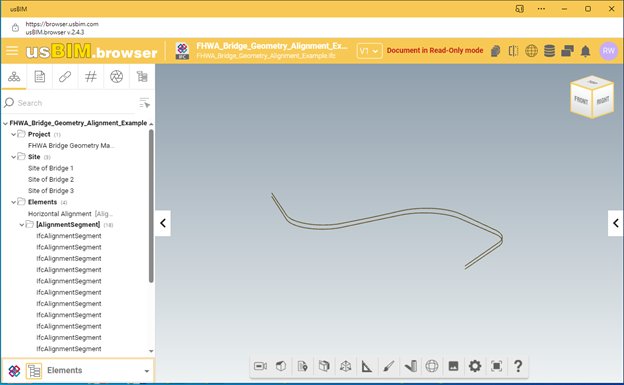
The generated IFC file may be viewed in any IFC viewer that supports IFC 4.3.2. Figures 9 through 11 show the alignment in viewers from ODA, ACCA, and Blender.
Summary[edit]
buildingSMART International’s IFC 4.3.2 schema has created exciting new opportunities for applying BIM concepts to all types of infrastructure projects. The IfcOpenShell toolkit has been updated to support the latest IFC specification, to emit geometric representations of alignments, and to evaluate linear placements and sectioned solids. This post has introduced alignment modeling with IfcOpenShell and provides example programs written in C++ and Python to illustrate the necessary details.
References[edit]
buildingSMART International. (2024, January 15). buildingSMART International. Retrieved from https://www.buildingsmart.org/
US Department of Transportation. (2022). Bridge Geometry Manual. Federal Highway Administration (FHWA). Washington, DC: FHWA. Retrieved from https://www.fhwa.dot.gov/bridge/pubs/hif22034.pdf